Batch 2 - Class 263 - Math in Genetics III - DNA Computing
(zoom)
Preclass Exercise:
- (Discussed in class)
Attendance: Advay, Raghav, Ayush, Aneesh, Shikhar, Rohan, Mihir, Vivaan, Aarkin, SiddhantJ, Kushagra, Vansh, Harshiet, Angad, Rehaan, Kabir, Siddharth
Class Notes:
Recap
- Genetic algorithms leverage the following principles of natural selection
- Hereditary transmission - for persistence of "good" variants
- Mechanism for variation - for example, cross-over, mutation, or diversity at starting point
- Survival advantage
- For example, coming up with "To be or not to be"
- More practical example: Box Car 2D.
Homework problem
Consider the maze below
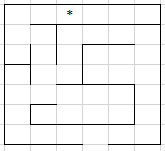
We are trying to find a path through the maze. Each path may be encoded as a sequence of "turns" - what does the path do when it encounters an obstacle (in absence of an obstacle, the path continues in a straight line). The actions might be L,R,B (left, right, back). Let us also say that the path has maximum length of 12 - i.e. if the path doesn't lead to "*" after 12 "turns" and encounters an obstacle, that path is over.
Think about how you would design a genetic algorithm to solve this. What would your coding look like? How will you introduce variation? How would you ensure that "good" features will persist? How will you define "fitness"?
If you know how to code, try to code this! Else try to run your "algorithm" on a random starting string, and see if the fitness scores improve from one generation to another.
Some possible lines of thinking
- Each path is an array of 12 turns, each turn being value L,R or B
- Start with a random selection of paths (4 paths should be good to start with, as long as they are not similar)
- At each generation, cross two paths - perhaps inherit alternate turns from each parent
- At some probability, say 10%, introduce a mutation - change a random turn to a random value (can skip initially)
- Fitness could be the maximum number of columns a particular path travels before dying
DNA Computers
Note that genetic algorithms do not really use DNA or genes - its just the principles of natural selection applied to computing and algorithms
One can actually use the DNA replication machinery present in living organism as a computer itself.
Why?
- Massively parallel - DNAs are always recombining in all possible orders
- Very small - a finger nail worth of DNA can encode 1 million CDs
- Cons - not very fast yet, and we have not built enough engineering expertise
Basics
- DNAs are made of four kinds of molecules A, T, G, C (adenine guanine cytosine thymine), so that A and T pair together and G and C pair together
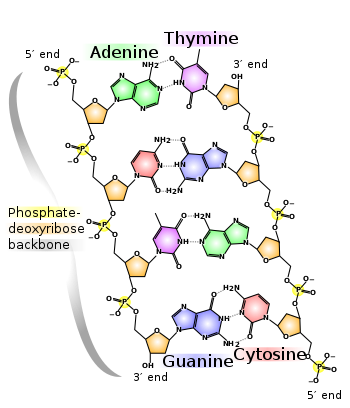
- Give kids some combinations and let them figure out the complementary strands
- These then form a whole chain
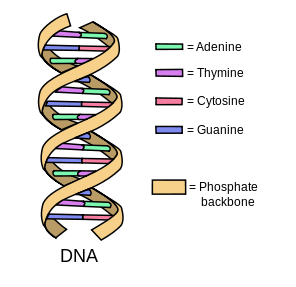
- So if we put fragments of DNA and mix them up, then they will start to combine with each other according to these rules, and hence be able to "compute"
- Similarly, we can use DNA for storage by storing these strands. If we want to copy it, we simply separate the strands and put them in a mixture of A, T, G, C and they will start to pair with the relevant molecules to create copies!
Lets see an example
- Leonard Adleman 1994 - solved the traveling salesman problem using DNA computing
- TSP: There is a salesman who needs to visit all the given cities in the shortest possible path without visiting the same city twice. TSP is an NP complete problem, i.e. we don't know how to solve it efficiently using classical computers - we pretty much have to try each combination and figure out which one is shortest
- With parallel computing, we can perhaps try out all the combinations in parallel, and then check for the shortest one!
- How could we do that using DNA? Let kids come up with some ideas, even if they are wrong
- Basic idea
- Each city is coded with 20 length DNA sequence, eg: ATCGGCTGCAGTCAACTCAG could be a city. The city codes are chosen carefully so that we don't repeat the codes for two cities
- Now what do we want to connect? Two different cities. How do we do that? We create complementary strands that are "edges" - they contain the latter half of one city and first half of second city - since we are trying to join those cities, we obviously want the complementary string
- So, for example, if the two cities were ATTG and TCGA, then if we join then we need TGTC and the complementary "edge" string would be ACAG. So this becomes our "glue" and we mix the city strands with all possible "glue" strands
- Give kids some other city combinations and ask them to work out the complementary edge sequence
- Now the biological machinery gets to work and starts joining these strands in all possible ways. Some of those are good solutions and some are not
.png)
- What are "good" solutions
- They have a length of 140 (discard very long and very short segments)
- They do not repeat cities (check for presence of all city strands)
- These checks are performed at the end of combining phase to come up with the solution
- What would you do if all cities were not at the same distance from each other?
- Similarly tic-tac-toe problem has been solved.
- Essentially the computer plays first.
- Each of the other eight positions have corresponding substrate and enzymes associated with them. Now, depending on what the human wants to play, the enzymes corresponding to that position are mixed with substrates of all other positions.
- Note that a particular cell must "light up" if two other defined enzymes are mixed with its substrate (Show in game of tic-tac-toe)
- This is the essential AND logic gate functionality implemented using DNA
- For "lighting up" the substrate strands have a florescent DNA at one end, and a suppressor at other end - so if the enzymes break up the strand, the test tube lights up due to flourescence
Homework:
- Can you tile a 6x6 grid with 2x1 dominos, so that there are no fault lines (i.e. any horizontal or vertical line has at least one dominos going across it?)
- Answer: Can't be done - each of 10 lines in 6x6 grid divides the region into two even areas, so at least two dominoes must cross it. So there must be at least 20 dominoes, but there are only 18
References:
Mathematical Puzzles, Geoffrey Mott-Smith